Electrical Potentials
in Aqueous Solutions
Electrical Potentials
Require Charge Separation
In reading 8.3.1, one might get the impression that the rules are different when one considers charges in vacuum, metals, or water. That is NOT the case. The difference has to do with energy components of the interactions. For example, to generate a net charge one needs to separate charges. The initial conditions are almost always a neutral structure. How are ions formed?
- Remove an electron from an ion…ionization…say H2 ↔ 2 H+ + 2e-
- Deprotonation of an acid…R-COOH ↔ R-COO- + H+
- Separate a cation from an anion….NaCl ↔ Na+ + Cl-
The ionization of an atom depends on the energy needed to remove an electron from an orbital. The energy to separate charges depends on the electrostatic attraction between ions. The dissociation of a carboxyl group depends on the energy of breaking that bond.
The latter 2 also depend on the interaction between the solvent (water, oil, ethanol…etc.) and the ions. The presence of water stabilizes the ions that are formed thus favoring ionization. The vacuum cannot do that. Hence the apparent difference in the “rules”.
Quantitative Measures
of the Degree of Ionization
Ionization by adding or removing an electron are reduction/oxidation reactions. You dealt with these in Chemistry. We will not address these any further.
Protonation and deprotonation reactions are quantitated by measuring the pK. Recall that pK is the negative log of the equilibrium constant. The fundamental expression is just a chemical equilibrium:
HA ↔ H+
+ A- and thus 
Note that the degree of dissociation (or ionization) depends on the concentration of the ions and that of the neutral specie. Why is that?
Also recall that the equilibrium constant is not quite constant.
It depends not only on the energy change in going from a neutral molecules to ions dissolved in water, but also on the thermal energy, RT. Think about how the temperature and the energy change involved in the dissociation affect the degree of ionization. Does it agree with your intuition? Does this last equation look like the Boltzmann Distribution? Do you see why it’s basically the same thing?
What about the dissociation of a salt? Well it is essentially the same thing:
NaCl ↔ Na+ + Cl- and thus 
However, since a solid has a concentration of 1, the equilibrium constant becomes the solubility product, Ksp.
Ksp = [Na+][Cl-]…where the concentrations are Molar concentrations
The uncharged solid is not soluble in water whereas the ions are. Thus dissociation is equivalent to solubility. Ionization here is also concentration and temperature dependent for the same reasons as above.
Electric Fields in
Water
Proteins in aqueous solution almost always carry a net charge. At the unique pH , called the isoelectric point, the net charge is zero. At this pH the number of positive and negative charges on the protein is equal. Thus there are still charges.
Question, if a protein is purchased as a powder and the powder was produced at a pH far away from the isolectric point, is the powder charged?
Do charged proteins in water affect each other? If charged they must generate an electric field. How far does this field extend?
Well, let’s begin at the beginning. What happens when a neutral protein is dissolved in water? Dissociable groups may pick up (lysine, arginine) or release (aspartate, glutamate) protons. Ion pair will dissociate. So there will be the protein and a variety of counterions. The total charge will be zero but individual ions will move in response of BOTH the electric field of other ions and thermal energy. These result in the protein and its counterions forming a loose grouping, sort of like a Navy battle group centered on an aircraft carrier….except with far fewer collisions. The distance between the protein and the counterions is a rough measure of the extent of the electric field emanating from the protein. Of course the counterions also produce an electric field. Now consider that, generally, the solution contains ions from other salts dissolved in water. The protein does not keep track of which ions are its original counterions and which came from other salts so there is free exchange of ions. The only requirement is that the protein plus the neighboring ions results is an essentially zero total charge. Yes, it’s all about charge. The presence of the counterions effectively neutralizes the protein. The more extraneous salts are present the more effective the neutralization…i.e. the neutralization takes place over a shorter distance. This is often referred to as ionic screening of charged objects (proteins, nucleic acids, membrane surfaces, whatever).
The Debye Length
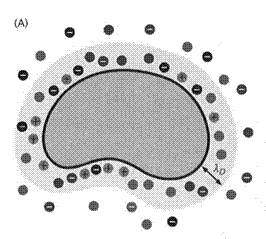A
protein surrounded by counterions is similar to a swarm of bees surrounding
someone who just disturbed their hive.
The bees are bussing around the victim. There are more bees close to the
person that farther away. The bees are not
static but moving in and out. Thermal
energy tends to disperse the counterions but the electric field attracts them
to the protein. The concentration of
counterions declines with distance just as the electrical potential declines
with distance. The counterions both
respond to the electric field coming from the protein and are responsible for
reducing this field.
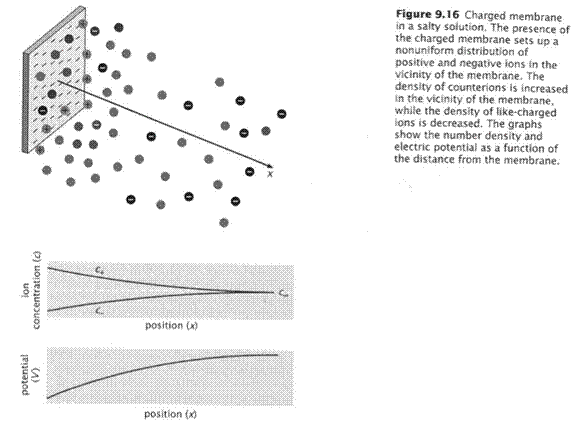
To examine this quantitatively it is useful to consider a 1-dimensional problem. Consider a uniformly charged flat surface, like the surface of a cell membrane but totally flat. The counterions will equilibrate almost instantly with the electric field, a dynamic equilibrium because there is constant motion. The electrical potential in the solution will decay with distance from the flat surface. The concentration of ions with distance must be in equilibrium with the electrical potential at any point. The ionic concentration at any distance from the protein (x) is expressed relative to a standard state…here it is the concentration far away from the protein (x = ∞) where the voltage is zero. We have pairwise comparisons: 2 distances, 2 energies, 2 concentrations. That’s the job of the
· Boltzmann distribution:
·
C is for the cations;
x is the distance from the protein surface
·
zc is the valency
of the cation; Vx is the voltage at
distance x
·
zFVx =>Volts*Coulombs/mole= J/mole
·
RT=Thermal energy/
mol
·
The potential acts on
both cations and anions
·
Considering a
negatively charged surface, the cations will tend to accumulate close to the
surface and the anions tend to move away from the surface (see figure). This figure is for monovalent cations and
anions.
Look at the
plot of voltage as a function of distance.
The slope of the curve at any point is the electric field (the
force). That field can only change if
there is a charge density (ρ, rho).
Indeed there is a charge density because the cation concentration is
greater than that of the anion. So, the
ions are driven by the field but they also reshape the field. Remember that the field is the result of the
effects of all the charges present and how they attract or repel each
other.
There is a relationship between charge
density, ρ, and the electric field, E (remember that 
):
…the Poisson equation
·
…since the valencies are opposite, the
concentrations will subtract leaving the charge density which is the
concentration of charge.
·
Using the Boltzmann
to substitute for the ionic concentrations and assuming monovalent ions:
·
…fitting
into the Poisson equation and solving for low potentials:
1/Κ= λD = length unit called “Debye Length”
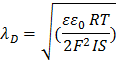
ε is the unitless
dielectric constant; ε0 = permittivity of
free space
IS= Ionic strength =
…where ci is the concentration of each ion and zi is the respective valency
… it has units of concentration and corrects for
the greater effect of polyvalent ions
·
the potential decays
exponentially with distance from the surface
·
Every Debye-length, the potential will decrease
by 1/e
·
The Debye Length diminishes as the square root
of the ionic strength
|
Ionic Strength |
Debye Length |
|
10 mM |
3 nm |
|
100 mM |
1 nm |
|
1 M |
0.3 nm |
·
-- more ions take the
place of the counter ions and thus the potential decays more rapidly with
distance from the charged surface
·
--- the more dilute, the
longer the Debye Length
·
The chemical potential of the cations does not
change with distance from the membrane. The concentration of the cation changes. Similarly for all mobile ions. At equilibrium there cannot be any change in
energy with distance.