Evolutionary Stable Strategies

I. What is an ESS (evolutionary stable strategy)?

A. ESS: a strategy which if adopted by all members of a population cannot be invaded by a mutant strategy through the operation of natural selection. (Note that a stategy is the behavioral phenotype of an individual, usually a composite of behaviors.)

B. Game theory is used whenever the evolutionary outcome is frequency dependent, i.e. whenever the fitness consequences of an act depend on what others in the population are doing, in other words competition occurs. Note that the ESS need not maximize fitness!

C. Assumptions:

1. Infinite population
2. Asexual (haploid) reproduction
3. All possible strategies have been specified
4. Either pairwise contests occur between two opponents or one individual competes against a group

II. Why don't animals injure each other more often during contests over resources? - The basic symmetric model for the evolution of display with equal opponents

A. Possible behaviors during a contest: display, escalate with risk of injury, or retreat

1. which cannot detect differences between themselves (i.e. the contest is symmetrical)

B. Possible strategies:

1. Hawk - escalate and continue until injured or until opponent retreats
2. Dove - display initially but retreat if opponent escalates.

C. Payoff matrix (changes in fitness due to interactions):

		Opponent:
		Hawk	Dove
Actor	Hawk	(V-C)/2	V
	Dove	0	V/2

V = value of resource being contested; C = cost of fighting due to injury

D. Possible solutions -

1. When V > C, Hawk is a pure ESS, i.e. Hawks can

a. resist invasions: the payoff to an individual adopting strategy I when confronted with an opponent adopting strategy I is greater than the payoff to an individual adopting strategy J when confronted with an opponent adopting strategy I

b. and invade: the payoff to an individual adopting strategy I when confronted with an opponent adopting strategy I is equal to the payoff to an individual adopting strategy J when confronted with an opponent adopting strategy I, and the payoff to an individual play I against J exceeds the payoff to an individual playing J against J

2. When V < C, hawks and doves coexist at a mixed ESS which occurs when the fitness of the two strategies are equal

a. assume p = proportion of Hawks in the population

b. fitnesses of hawks and doves:

W(H) = p[1/2(V-C)] + (1-p)(V)
W(D) = p(0) + (1-p)(V/2)

c. Thus, W(H) = W(D) =p/2(V-C) + (1-p)V = (1-p)V/2 or p = V/C. Consequently, we expect escalation to occur only if the benefit of the resource is greater than the risk associated with fighting for it.

d. Mixed ESS can occur by two mechanisms:

i. a stable strategy set in which a single individual sometimes performs one strategy and sometimes another with a fixed probability, p.

ii. a stable polymorphic state: a fraction, p, of the population adopts one strategy while the remainder, 1-p, adopts another.

e. Alternative reproductive strategies which appear to be mixed ESS

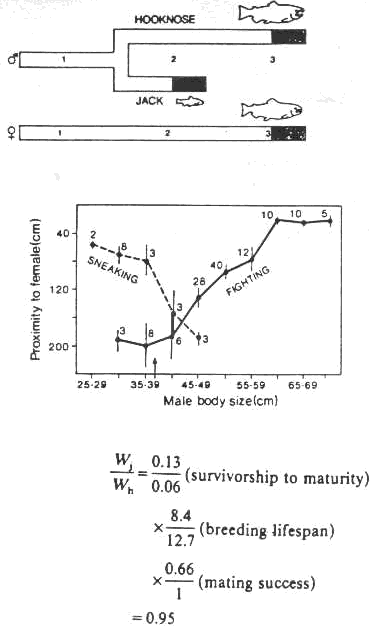
i. Hooknose and jack salmon

ii. Bluegill sunfish

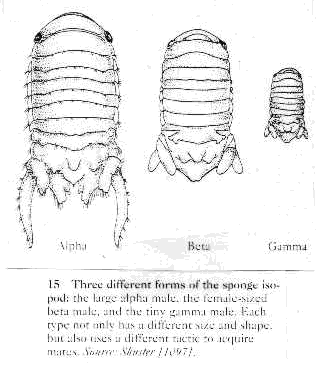
iii. marine isopods (see text)

iv. Soay (bighorn) sheep
v. Ruff (lekking shorebird)

f. Alternative reproductive strategies which appear to be condition dependent strategies, i.e. males make the best of a bad situation

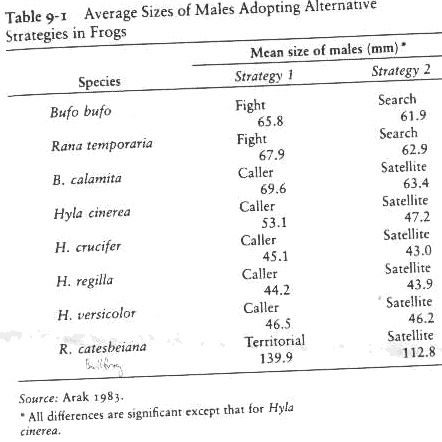
i. Caller and satellite male frogs

ii. Horned and hornless male beetles


3. In general, for the matrix:

	I	J
I	a	b
J	c	d

a. There is a stable mixed ESS when c > a and b > d and an unstable ESS when a > c and d > b.

b. A game with only 2 pure strategies has at least 1 ESS, but in games with 3 or more pure strategies, no ESS need exist

III. Asymmetric contests in which payoffs are uncorrelated with phenotype, i.e. opponents are arbitrarily unequal

A. Hypothetical example: Hawk - Dove - Bourgeois

1. Bourgeois strategy => if owner play hawk, if intruder play dove
2. Payoff matrix assuming owner and intruder are equally frequent and get equal payoffs

	H	D	B
H	(V - C)/2	V	3V/4 - C/4
D	0	V/2	V/4
B	(V - C)/4	3V/4	V/2

3. If V > C, then H is pure ESS; if V < C then B is pure ESS
4. Conclusion: there is no need for differences in payoffs before asymmetries will solve contests
5. Example - speckled wood butterflies (see text)

IV. Single correlated asymmetry with uncertain information, Hawk - Dove - Assessor (this example was not discussed in lecture)

A. Assessor - chooses Hawk if has higher resource holding potential (RHP), Dove if smaller

	H	D	A
H	(V - C)/2	V	(V-C)/2
D	0	V/2	V/4
A	V/2	3V/4	V/2

B. For this game, assessor is ESS, but if we assume there is a cost of assessment, c, and x is the probability of the larger animal winning an escalated contest, then assessor is the ESS for some parameter values while hawk is the ESS for others.

C. Example: damselflies which win contests have higher fat reserves

V. Sequential assessment

A. Assumptions

1. Animals display in order to acquire information about each other's fighting ability and resource value, e.g. red deer

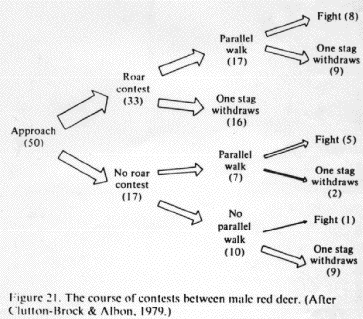
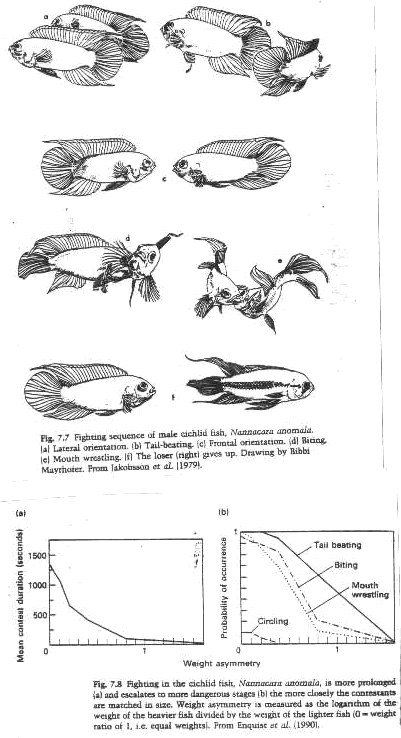
2. If an animal can tell it is unlikely to win a contest, it will not engage in a fight unless it values the resource highly. When two individuals are closely matched and resources are of equal value, fights will occur.

B. Predictions

1. The length of a fight should increase when the asymmetry in fighting ability decreases
2. The cost of a fight should increase when the asymmetry in fighting ability decreases
3. An individual's probability of winning should increase as the asymmetry in fighting ability increases

C. Examples - cichlids

Brockman, H. J., A. Grafen & R. Dawkins 1979 Evolutionary stable nesting strategy in a digger wasp. J. Theor. Biol. 77: 473-496.

Chase, I.D., Barolomeo, C. & L. Dugatkin 1994 Aggressive interactions and inter-contest interval: how long do winners keep winning? Anim. Behav. 48:393-400.

Clutton-Brock, T. H. & S. D. Albon 1979 The roaring of red deer and the evolution of honest advertisement. Behaviour 69: 145-170.

Davies, N. B. & T. M. Halliday 1978 Deep croaks and fighting assessment in toads, Bufo bufo. Nature 274: 683-685.

Davies, N.B. 1978 Territorial defence in the speckled wood butterfly (Pararge aegeria): the resident always wins. Anim. Behav. 26: 138-147.

Enquist, M. and O. Leimar 1983 Evolution of fighting behavior: decision rules and assessment of relative strength. J. Theor. Biol. 102:387-410.

Grafen, A. 1987 The logic of divisively asymmetric contests: respect for ownership and the desperado effect. Anim. Behav. 35:462-467.

Gross, M.R. & E.L. Charnov 1980 Alternative male life histories in bluegill sunfish. Proc. Natl. Acad. Sci. USA 77:6937-6940.

Gross, M.R. 1985 Disruptive selection for alternative life histories in salmon. Nature 313: 47-48.

Hammerstein, P. 1981 The role of asymmetries in animal contests. Anim. Behav. 29:193-205.

Hammerstein, P. and S. E. Riechert 1988 Payoffs and strategies in territorial contests: ESS analyses of two ecotypes of the spider Agelenopsis aperta. Evol. Ecol. 2:115-138.

Lank, D.L., C.M. Smith, O. Hanotte, T. Burke and F. Cooke 1995 Genetic polymorphism for alternative mating behavior in lekking male ruff Philomachus pugnax. Nature 378:59-62.

Leimar, O. and M. Enquist 1984 Effects of asymmetries in owner-intruder interactions. J. Theor. Biol. 111:475-491.

Leimar, O., S. Austad, and M. Enquist 1991 A test of the sequential assessment game: fighting in the bowl and doily spider Frontinella pyramitela. Evolution 45:862-874.

Marden, J.H. & J.K. Waage 1990 Escalated damselfly territorial contests are energetic wars of attrition. Anim. Behav. 39:954-959

Marden, JH. & R.A. Rollins 1994 Assessment of energy reserves by damselflies engaged in aerial contests for mating territories. Anim. Behav. 48: 1023-1030.

Marrow, P., J.M. McNamara, T.H. Clutton-Brock 1996 State-dependent life history evolution in Soay sheep: dynamic modelling of reproductive scheduling. Phil. Trans. R. Soc. Lond 351:1335.

Maynard Smith, J. & G.A. Parker 1976 The logic of asymmetric contests. Anim. Behav. 24:159-175.

Maynard Smith, J. & G.R. Price 1973 The logic of animal conflict. Nature 246:15-18.

Maynard Smith, J. 1982 Evolution and the theory of games. Cambridge University Press, Cambridge.

Parker, G. A. and E. A. Thompson 1980 Dung fly struggles: a test of the war of attrition. Behav. Ecol. Sociobiol. 7:37-44.

Parker, G. A. 1984 Evolutionary stable strategies. In: Behavioral Ecology. 2nd Ed. (J. R. Krebs & N. B. Davies, eds.) Sinauer, Sunderland.

Parker, G.A. & J. Maynard Smith 1990 Optimality theory in evolutionary biology. Nature 27-33.

Shuster, S.M. and M.J. Wade 1991 Equal mating success among male reproductive strategies in a marine isopod. Nature 350:608-610.

Turner, G.F. & FA. Huntingford 1986 A problem for game theory analysis: assessment and intention in male mouthbrooder contests. Anim. Behav. 34:961-970