Distance Methods

A phylogenetic tree with branch lengths implies a large number of distances among pairs of taxa. Distance methods attempt to reconstruct the tree by first determining the distance among all pairs of taxa in the study, and then finding the tree that best explains these distances.

There are many ways to determine the distances, and many ways to find the corresponding tree. Consequently distance methods constitute a complex family of methods.

Consider a tree with only two taxa

What meaningful information is available in such a case?

Because there are only two taxa, there is only one possible tree topology, but the length of the branch still contains useful information.

The distance between two taxa is essentially a two-taxon tree

The simplest measure of distance is a simple count of mis-matched characters, possibly divided by the length of the sequence. This gives the fractional difference, which is a crude measure of the branch length

When the number of differences is very small (in proportion to the number of characters that are expected to vary), then this provides an acceptable measure of branch length

When the number of differences becomes large, such that some characters have undergone multiple substitutions, then one expects that superimposed changes have occurred, and the measure of branch length becomes unreliable.

Better measures of distance take into account the expectation of multiple superimposed substitutions. Such corrected distance methods can perform very well.

Finding the best tree given distances

Tree-additive distances

Assume that distances correspond to a tree topology connecting the taxa

Branch lengths are free to vary

Ultrametric distances

More restrictive than tree-additive distances

Every common ancestor is equidistant from all descendants

Not consistent with what is known of sequence evolution, but may be useful for describing similarity in a non-evolutionary context

If life were easy, there would be no conflict between distances calculated for several pairs of taxa

The tree could be constructed quickly and unambiguously by comparing the distances between taxa

Place most closely related pair of taxa together

Join the next most closely related pair of OTUs (operational taxonomic units); these might be either another pair of taxa, or a taxon and a set of taxa that had already been grouped.

Continue joining taxa until the tree is built

This general process is called star decomposition

Unfortunately, life is not easy, and there are usually discrepancies between calculated pairwise distances

The optimal tree corresponding to distance data will be the tree that minimizes these discrepancies.

Find the tree topology that minimizes a measure of the discrepancy between the distance between taxa measured along branches of the tree and the observed distance between the taxa.

Several such measures of error are available, but the most commonly used ones are closely related.

The Fitch-Margoliash approach (text p. 448)

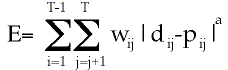
E is error fitting distances to tree

T is the number of taxa

wij is the weight varying with separation of taxa

dij is the pairwise distance estimate

pij is the distance between i and j on the tree

For weighted sum of errors, a = 1, weighted squared errors, a=2

Unweighted sum of errors

wij = 1 (Cavalli-Sforza and Edwards, 1967)

Assumes that all distance measurements (both long and short) are similarly reliable.

Weighted sum of errors

wij=1/dij² (Fitch and Margoliash, 1967)

Assumes that the error is a fixed proportion of the total distance

wij = 1/dij (Felsenstein, 1993)

Weight in inverse proportion to the distance

Less sever than Fitch-Margoliash)

wij=1/sigmaij²

Where sigma is the expected variance for the distances

Nice if variance can be estimated

Note that special handling is necessary for identical sequences

Other weightings would also be possible

Weighted sum of errors squared

As above, but a=2

Places emphasis on outlying measurements

Minimum Evolution

Fit branch lengths with unweighted least-squares (wij=1, a=2)

Calculate the tree's goodness of fit by summing the length of each branch on the tree (called LS length)

Minimum evolution works well in simulation studies

Algorithmic Distance Methods

Overview

Do not find an optimal tree

Build tree, but do not perform any branch swapping

Do not explicitly incorporate any optimality criterion

Can be useful (if their assumptions are justified) to find starting trees for subsequent branch swapping, and for very rapid exploratory analysis.

We have already discussed stepwise addition, the algorithm that can be used to build a starting tree during heuristic searches in a wide variety of optimality methods.

UPGMA

Assumes ultrametric distances

Neighbor Joining

Does not assume ultrametricity