Measuring Edge Responses

The best approach to measuring edge responses has been a topic that has received a great deal of attention in the edge literature (Ries et al. 2004). The most common topic of debate has been the best way to capture the non-linear dynamics that result from the threshold nature of edge effects (that edge effects are expected to extend only a limited distance into habitat, thereafter leveling off in the habitat’s “core”). Several approaches have been proposed, although none of them has 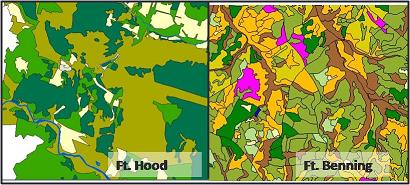become commonly used. Further, only one of these proposed models (Malcolm 1994) address the critical assumption of most edge studies, which is that the best metric for describing edge effects is the distance to the closest edge. This assumption allows researchers to ignore the complex geometry that is usually found in most landscapes (see sample maps from our study sites: Forts Hood and Benning). Further, these maps highlight that, in contrast to the dominant conception as an edge being the coming together of two habitats, there are often multiple converging habitats at a single point. This actually presents two challenges in measuring edge responses in the field. The first is determining the maximum distance of edge influence (hereafter, Dmax). This critical measure is useful for almost any application of edge study. How deep do edge effects go? How large do patches have to be to include "core" area - and how much "core" are is there. So even the simplest application or consideration of edges relies on knowing this, and it is rarely measured in a rigorous way (ref).

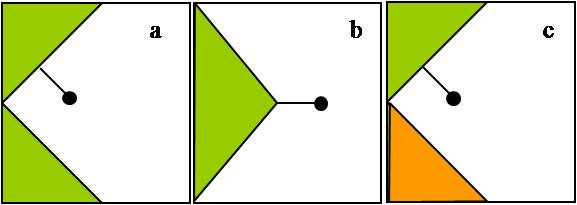The second challenge is testing the assumption that edge effects are best described by distance to the closest edge. Surprisingly, there has been very little research examining the consequences of violating this assumption, even though logic would seem to suggest that it may not be true. For instance, it seems reasonable to expect edge responses to be stronger when in a corner (a) or weaker when outside a corner (b). But even this has rarely been tested (but see Fletcher 2005). Even more surprising, we are aware of no study that examines what happens when three habitats converge at a common edge (c). Despite this dearth of studies on the impacts of patch geometry and the convergence of multiple habitat types, these features are ubiquitous in most landscapes (see maps above).

The model proposed by Malcolm (1994) uses line integrals to consider the effect of all nearby edges on the ecological response at any point within a patch. We have found that this approach offers two distinct advantages over other candidate models. The first is that the model returns a parameter that specifies the distance of maximum influence (Dmax) and assumes that density levels off after that (i.e., in the "core" of the habitat). This is consistent with the most basic assumptions 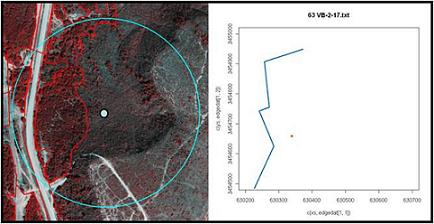about how edges operate and, unlike other approaches, the identification of Dmax is very precise. The second is that it can consider the unique geometry of each patch in estimating (or extrapolating) edge responses. Because the researcher is able (but not required) to map out the geometry of each patch and code that into the model, the assumption that edge shape is not important can be explicitly tested. However, the intensive mathematics required to use the model is likely the reason it has never been applied. To eleviate that barrier, we have developed an R-package ("edgefx") that applies the model and performs all necessary mathematical operations if the researcher provide a map of the line segments (see example to right). Finally, while Malcolm's original model does not consider the convergence of multiple habitat types, there is no reason it can not be expanded to do this (although we have not done so yet).

The basics of Malcolm's model

Download the R-package ("edgefx")

View a guide to the R-package ("edgefx")

Selected references showing other approaches to measure edge effects:

Ewers and Didham 2006

Fletcher 2005

Toms and Lesperance 2003